Demystifying the Cross Product

Have you ever wondered how robots grasp objects perfectly or self-driving cars navigate busy intersections? The answer lies in the fascinating world of linear algebra, where two essential tools dance hand-in-hand: the dot product and the cross product. While the dot product measures similarity, the cross product adds a crucial ingredient – direction.

Today, we'll embark on a journey to understand the cross product and its remarkable role in the realm of Artificial Intelligence (AI).

What is Cross Product?

The cross product is a mathematical operation that takes two vectors and produces a third vector perpendicular to both. Think of it as a way to combine two directions to find a new direction that's at right angles to the original pair.

How does the Cross Product work

To compute the cross product of two vectors, we use a formula that involves multiplying the components of the vectors and then taking their differences. The resulting vector is perpendicular to the plane formed by the original two vectors.

For example, if you have vector a and vector b, and you calculate their cross product:  c = a × b. 

The direction of c will tell you whether you need to rotate vector a clockwise or counterclockwise to align it with vector b.

Cross Product: The Dot Product’s Partner

The dot product assesses the closeness or strength of relationship between vectors (works like a measuring tape). However, it lacks directionality, making it unable to guide navigation.

This is where the cross product comes in, acting as a compass by providing the necessary direction/rotation to align vectors.

Together, they empower AI to sense and navigate the world with precision. From flawless object manipulation by robots to collision avoidance in self-driving cars, this partnership is the key to their remarkable capabilities.

Cross Product in Action: An Example!

Consider a scenario where a robotic arm needs to grasp an object. The robotic arm's orientation vector is represented by a, and the object's orientation vector is represented by b.

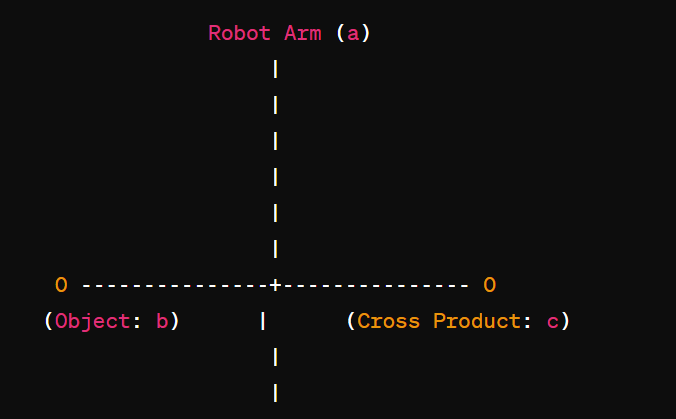
In this simplified visual representation:

• The robotic arm's orientation vector a and the object's orientation vector b define a plane.

• The cross product c yields a third vector perpendicular to this plane.

• The direction of c indicates the direction of rotation needed for the robotic arm to align itself with the object, ensuring accurate grasping or assembly.

• Depending on the direction of c, the robotic arm can determine whether it needs to twist clockwise or counterclockwise to achieve the desired orientation.

Putting it Together: Matrices in Machine Learning!

Matrices are the building blocks of linear algebra, a powerful mathematical language used in many AI and ML algorithms. By understanding matrices, you gain a deeper appreciation for how AI "thinks" and solves problems.

Deepen Your Understanding with De-Bug!

Curious to explore more? Stay tuned for upcoming newsletters where we dive into practical AI applications. We break down complex concepts into relatable examples and deliver them straight to your inbox.

Join us and become an AI insider, equipped to navigate this ever-evolving field!